 |
|||
|
Informazioni
pratiche Informazioni
scientifico-didattiche |
|||
 |
|
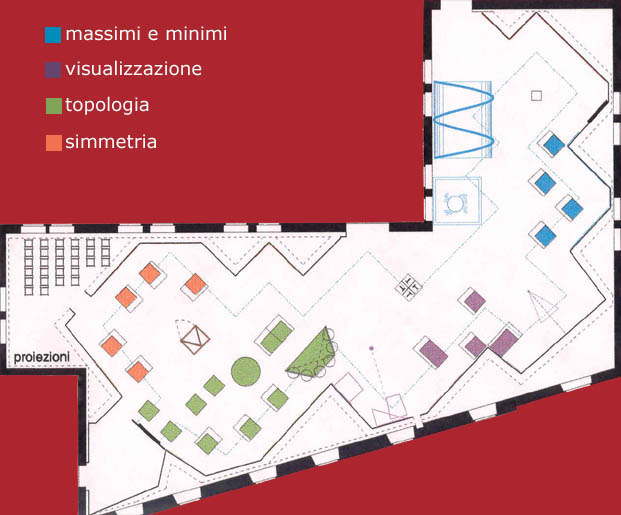
La mostra si apre con alcuni flash su realtà scientifiche e/o produttive di Milano o del suo immediato hinterland. Essi si propongono di offrire, senza pretese di completezza, alcuni esempi di applicazioni della matematica alla vita di tutti i giorni e di suscitare nel visitatore sia sorpresa verso aspetti della disciplina a priori molto lontani dall'immaginario dei non addetti ai lavori sia interesse verso le acquisizioni della matematica di base illustrate nel resto dell'esposizione. Capita
a tutti di cercare la via più breve per andare da un posto
a un altro o di voler spendere il meno possibile per gli acquisti:
la vita quotidiana è una continua ricerca del minimo sforzo
per ottenere il massimo risultato. Questa ricerca assume particolare
rilevanza in ambito scientifico e tecnologico, dove spesso i modelli
usati per descrivere fenomeni e progettare strutture si basano su
principi di minimo o massimo. E' possibile ricostruire con esattezza un oggetto tridimensionale avendo come unico dato la sua rappresentazione bidimensionale? Quali sono le difficoltà da affrontare per ricostruire un oggetto reale a partire da una sua immagine? La sezione visualizzazione ci aiuta a trovare le risposte a queste domande e a mostrare con vari esperimenti come la sola visione non sia sufficiente per ricostruire gli oggetti di partenza. Ci sono situazioni in cui non hanno più importanza la forma e la dimensione di un oggetto, o la lunghezza di un itinerario, ma solo fattori in un certo senso più "di base", proprietà degli oggetti che non cambierebbero anche se questi fossero fatti di gomma e li si potesse distorcere a piacere (senza romperli). La disciplina che se ne occupa è la topologia e gli esperimenti della terza sezione si propongono di dare un'idea di che cosa ciò significhi in due ambiti apparentemente molto lontani fra loro: uno relativo ai nodi e un altro che prende spunto dalla pianta di Milano. Una chiave di lettura fondamentale che si usa continuamente (in maniera più o meno consapevole) per interpretare i messaggi più disparati che provengono dal mondo circostante è quella della simmetria. Le esperienze della quarta sezione del percorso sono state progettate per evidenziare e far riconoscere al pubblico i diversi tipi di simmetria (ma anche le rotture di simmetria!) che si possono rintracciare nei monumenti, nelle opere d'arte e nei complementi di arredo urbano di Milano e dintorni. Ciascuna
sezione comprende inoltre una parte virtuale, con animazioni di
diverso tipo (interattive e non) che propongono al visitatore ulteriori
aspetti relativi ai temi trattati. Si potrà così –
fra le altre cose – assistere al “film” con cui da
otto cubetti si passa alla sfera di pari volume (massimi e minimi),
entrare nel quadro di Piero della Francesca per controllare le ipotesi
fatte sulla disposizione di alcuni oggetti (visualizzazione), vedere
come la mappa della Milano cinquecentesca a forma di decagono si
trasporti su un doppio toro (topologia), costruire fregi e mosaici
a piacimento o provare a identificarli (simmetria). A
partire dal mese di ottobre, l’esposizione sarà completata
da un’installazione visuale composta da un cortometraggio e
da alcune interviste nelle quali artisti e professionisti del territorio
milanese illustrano come la matematica intervenga nella loro attività. |
