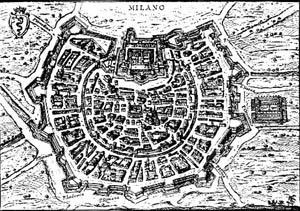
La pianta di Milano, come quella di molte città di pianura, ha una forma approssimativamente circolare: attorno a un nucleo centrale sono evidenti i cerchi concentrici che testimoniano i successivi accrescimenti della città nel corso dei secoli. Una possibile interpretazione di questo fatto può ricercarsi nella proprietà isoperimetrica del cerchio: fra tutte le figure piane aventi perimetro dato, il cerchio ha l'area maggiore o, equivalentemente, tra tutte le figure piane aventi un'area di valore assegnato è quella di perimetro minore.
La forma circolare di una cinta muraria rende minima la parte esposta a possibili aggressioni esterne, offrendo allo stesso tempo il maggior spazio per lo sviluppo urbano.

Nel primo exhibit si può avere evidenza sperimentale di questa proprietà: dando una forma arbitraria ad un nastro flessibile e riempiendolo di palline, si osserva che esso tende ad assumere una forma circolare.

Se, invece di considerare tutte le figure piane, ci si limita a considerare soltanto i rettangoli, qual è la soluzione del problema "area massima a perimetro costante"? La risposta si può trovare sperimentalmente con l'ausilio di alcune corde chiuse di lunghezza fissata, che si possono tendere sulle maglie di una scacchiera: è quanto viene proposto da un secondo tavolo di esperimenti.
Una variante di questo problema prevede di costruire ancora un rettangolo di area massima, utilizzando questa volta una cordicella aperta e parte del bordo della scacchiera. Se con uno specchio posto sul bordo si riflette uno di questi rettangoli, si ottiene un rettangolo di area doppia delimitato da una cordicella chiusa di lunghezza doppia. Questa osservazione permette di interpretare le nuove soluzioni per mezzo di quelle del problema precedente.

Nel terzo exhibit, utilizzando delle tessere a forma di triangolo equilatero, si può provare a risolvere la versione "simmetrica" delllo stesso problema: tra tutte le figure che hanno una determinata area, qual è quella di perimetro minore?
Se ci fosse assoluta libertà nella costruzione, la soluzione sarebbe il cerchio, ma le forme costruibili accostando un certo numero di tessere non possono essere circolari. Tuttavia le soluzioni sembrano rispondere ad un ipotetico "principio della maggior circolarità possibile".

Se alle figure piane si sostituiscono oggetti tridimensionali, il problema isoperimetrico può essere riformulato chiedendo quale sia la figura tridimensionale che a parità di volume abbia la minore superficie esterna, oppure quale sia la figura che a parità di area esterna abbia il maggior volume. A suggerire che in questo nuovo contesto la sfera gioca il ruolo ricoperto prima dal cerchio, nella mostra è presente una delle famose sfere dello scultore Arnaldo Pomodoro.

Si ottengono figure dello stesso volume se accostiamo tra loro (faccia contro faccia) otto cubi della stessa grandezza. Quanto vale l'area della superficie esterna del solido che volta a volta otteniamo? Quale composizione dei cubi rende minima tale area?
Su un tavolo vengono messi a disposizione del visitatore alcuni cubi che possono essere accostati ad incastro per ricostruire i modelli tridimensionali di alcune composizioni raffigurate in un poster. Analizzando i diversi casi possibili si può facilmente dare risposta alle domande.

Qual è la rete stradale più breve che collega un certo numero di città? Come si può costruire una rete telefonica che sia la più breve possibile? Sono problemi che possono rientrare nella formulazione unitaria: dati alcuni punti nel piano, quali sono le reti di lunghezza minima che li collegano? Già quando i punti assegnati sono i vertici di un triangolo equilatero o di un quadrato, la soluzione non è affatto immediata. Su un tavolo vengono proposte alcune reti da misurare, confrontare e tra
le quali cercare la migliore.

Se dal piano passiamo di nuovo allo spazio, si può riformulare il problema precedente chiedendo quale sia la superficie di area minima che ha come contorno una fissata curva dello spazio. Le lamine di sapone, vincolate ad appositi telai metallici, tendono a formare configurazioni di area minima, alcune delle quali sono illustrate nei poster e in una composizione dello scultore Michele Ciribifera.

A completare le esperienze concrete suggerite in questa sezione, sulle postazioni informatiche si trovano animazioni e applicazioni interattive che, fra l'altro, mostrano alcune superfici minime (anche quelle non realizzabili con le lamine di sapone) e la maniera in cui - mantenendo costante il volume - il cubo si trasforma nella sfera.