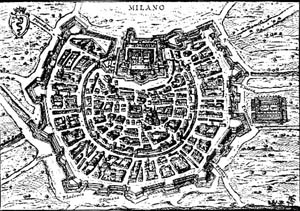
The plan of Milan, as well as the plan of other towns on the plain, is a circle approximately: the concentric rings that surround a central core are evident and testify the progressive increase of the town over the centuries. One of the possible interpretations of this shape is the isoperimetric property of the circle: the circle, among all the plane figures with a given perimeter, is the one which contains the largest area, or in a comparable way, among the plane figures with a given area, is the one with the shortest perimeter. The two problems are in fact equivalent.
The circular shape of the walls of a town reduces the surface exposed to possible assaults to a minimum and, at the same time, allows to have the largest area for urban development.

In the first exhibit it is possible to test this property: if you give an arbitrary shape to a flexible ribbon and you fill it with little balls, you can see that it takes a circular shape.

Now, let's consider rectangles only, instead of taking into account, as above, all the figures of the plane: what is the solution of the problem "maximum area at constant perimeter"? One can find an experimental answer thanks to some closed little strings of a given length, that it is possible to stretch across a chessboard : here is the proposal of another table of tests.
Another version of this problem is to build a maximum area rectangle once again, this time by means of an open little string and one part of the chessboard perimeter. If you reproduce one of these rectangles, by means of a mirror placed on the edge, you would see a double area rectangle, bounded by a double length little string. This observation allows new solutions to be interpreted by means of the previous problem.

In the third exhibit, one can try to find the solution of the "symmetric" version of the problem thanks to equilateral triangle shaped tesserae: which is the figure with the shortest perimeter among all those having a given area?
The solution would be a circle if the building was completely free, but shapes that one can build by putting a given number of tesserae near, cannot be circular. However solutions seem to answer a hypothetic "principle of the largest possible circularity".

Let's replace plane figures with tridimensional objects: the terms of the isoperimetric problem can be redefined by demanding what is the kind of tridimensional figure that, volume being equivalent, has the minimum exterior surface, or what is the figure that, exterior area being equivalent, contains the largest volume. One of the famous spheres by Arnaldo Pomodoro - sculptor - is shown at the exhibition just to suggest that in this new context the sphere is playing the role once hold by the circle.

Let's put eight cubes of the same size near (one face against the other one): how much is the area of the exterior surface of the solid we are each time creating? What kind of cube composition reduces this area to the minimum size?
Some cubes, that can fit into place to rebuild the tridimensional models of some compositions represented on a poster, are placed on a table at the visitor's disposal. It is easy to answer this question by analysing different possible cases.

What is the shortest road network linking a given number of towns? How is it possible to build the shortest telephone network? These problems can be included in a coherent formulation: given some points on a plane, what are the minimum length networks connecting them? Some networks to be measured are proposed on a table: it is possibile to realize that solutions aren't direct ones, already in case points are vertices of an equilateral triangle and of a square.

Let's move from plane to space. It is possible to formulate the previous problem again, by demanding which is the minimum area surface surrounded by a fixed curve in the space. Soap films, placed on peculiar metallic frames, tend to form minimal surfaces.
Some of them are illustrated in posters and in one composition by Michele Ciribifera - sculptor.

The practical experiences, suggested in this part, are completed on the workstation by animations and interactive applications that, besides, show some minimal surfaces (even those that can't be created by soap films) and the way the cube is turning into a sphere, the volume being constant.